Programming a Proportional Integral Controller

Now lets get started and talk about the goal of this quiz and what your expected results are to look like!
In the following quiz we will be building a proportional integral controller for regulating the altitude of a quad copter. You will need to follow along with the interactive comments in the code in order to build out the controller.

You want to shoot to have your output look like so:

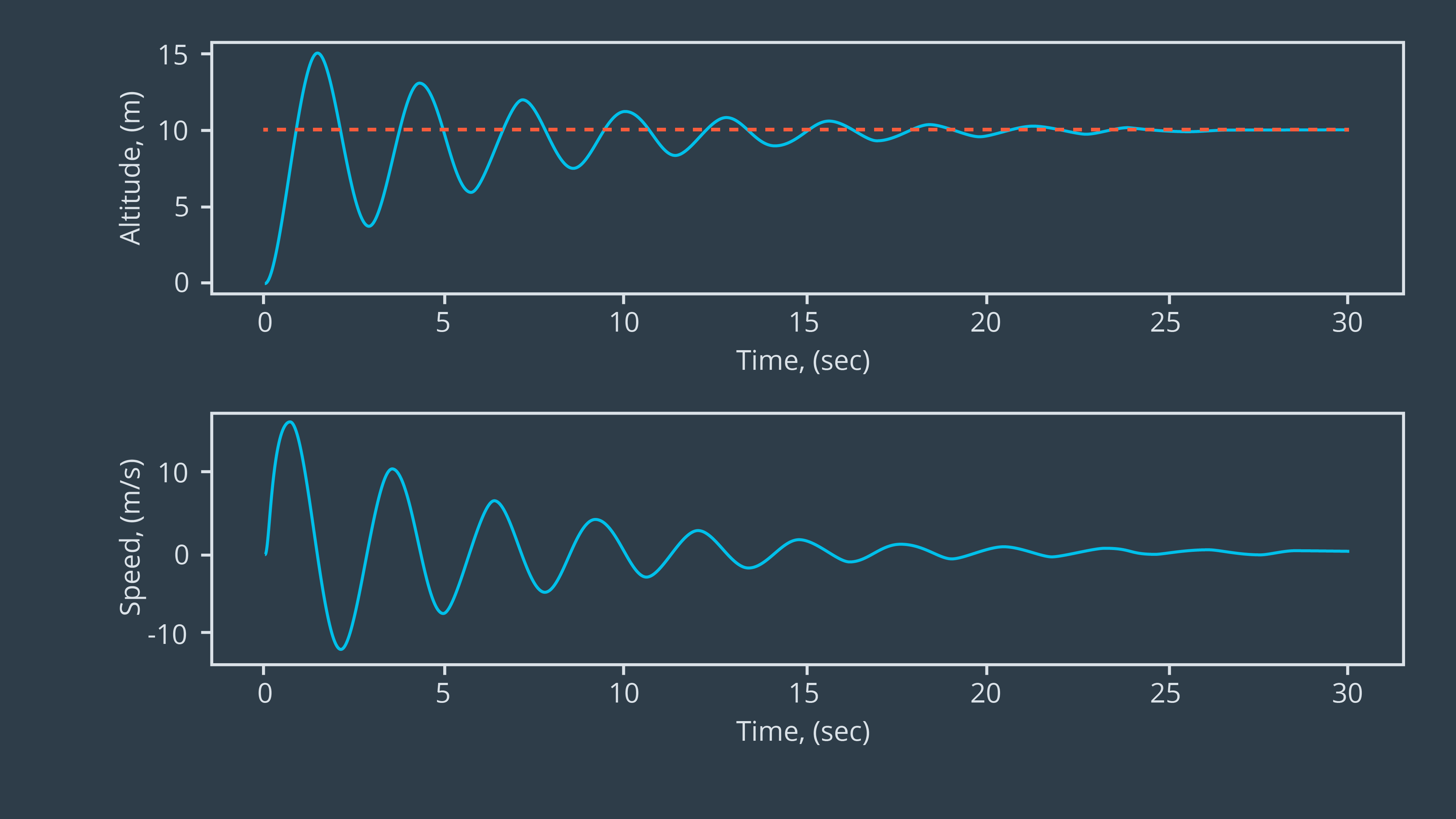
Where you can see that we are oscillating closer to the set point.

Be sure to spend sometime playing around with Ki (the integral constant) and see its effects one the altitude controller.

Ask your self the questions:

What happens when Ki is large?
What happens when Ki is small?
Do we reach our desired goal?
How does control effort vary with different Ki values?
How does the steady state offset and overshoot vary with different Ki values?

You can see below the desired control effort for this controller. Does it look efficient?

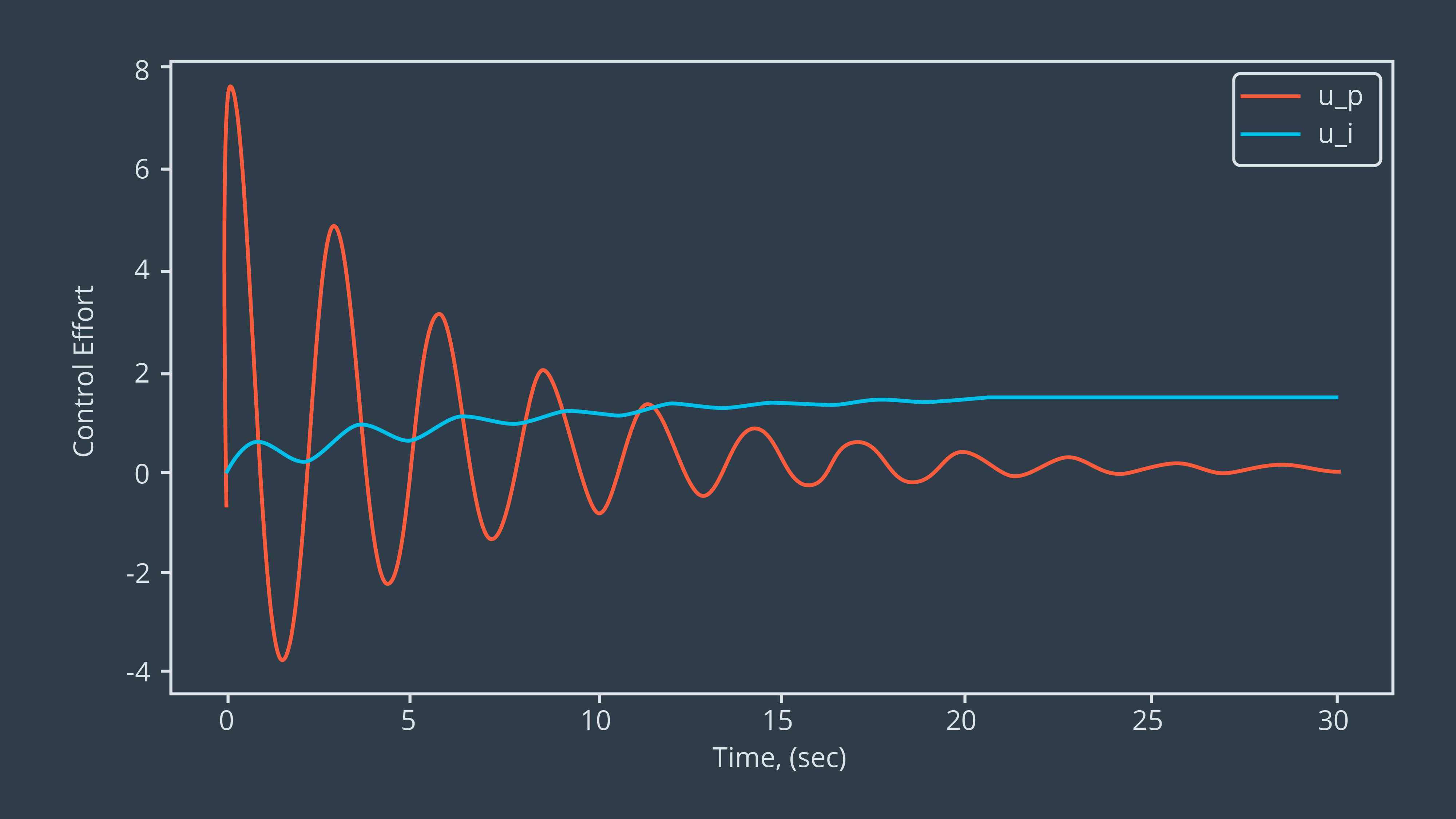
Keep these questions in mind as we progress through these quizzes and observe the positive and negative aspects of having or not having various controller components.

Start Quiz:

hover_plot.py pi_controller.py quad1d_eom.py solution.py

import numpy as np
import matplotlib.pyplot as plt
from pi_controller import PI_Controller
from quad1d_eom import ydot

##################################################################################
##################################################################################
# This code is what will be executed and what will produce your results
# For this quiz you need to set ki below to your desired value
# Then modify pi_controller.py to build out your PI controller
kp = 0.76
ki = 0.10
# Note that ki needs to be set to 0.10 in order to pass the project
# You are encouraged to change Ki in order to observe the effects
# What happens when Ki is really small?
# What happens when Ki is really large?
# Do we notice anything relating Ki and the control effort?
# Observe the steady state offset and the percent overshoot!
##################################################################################
##################################################################################

# Simulation parameters
N = 500 # number of simulation points
t0 = 0  # starting time, (sec)
tf = 30 # end time, (sec)
time = np.linspace(t0, tf, N)
dt = time[1] - time[0] # delta t, (sec)

##################################################################################
# Core simulation code
# Inital conditions (i.e., initial state vector)
y = [0, 0]
   #y[0] = initial altitude, (m)
   #y[1] = initial speed, (m/s)

# Initialize array to store values
soln = np.zeros((len(time),len(y)))

# Create instance of PI_Controller class
pi = PI_Controller()

# Set the Kp value of the controller
pi.setKP(kp)

# Set the Ki value of the controller
pi.setKI(ki)

# Set altitude target
r = 10 # meters
pi.setTarget(r)

# Simulate quadrotor motion
j = 0 # dummy counter
for t in time:
    # Evaluate state at next time point
    y = ydot(y,t,pi)
    # Store results
    soln[j,:] = y
    j += 1

##################################################################################
# Plot results
SP = np.ones_like(time)*r # altitude set point
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(time, soln[:,0],time,SP,'--')
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Altitude, (m)')

ax2 = fig.add_subplot(212)
ax2.plot(time, soln[:,1])
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Speed, (m/s)')
plt.tight_layout()
plt.show()

fig2 = plt.figure()
ax3 = fig2.add_subplot(111)
ax3.plot(time, pi.u_p, label='u_p', linewidth=3, color = 'red')
ax3.plot(time, pi.u_i, label='u_i', linewidth=3, color = 'blue')
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Control Effort')
h, l = ax3.get_legend_handles_labels()
ax3.legend(h, l)
plt.tight_layout()
plt.show()
##################
y0 = soln[:,0] #altitude
rise_time_index =  np.argmax(y0>r)
RT = time[rise_time_index]
print("The rise time is {0:.3f} seconds".format(RT))

OS = (np.max(y0) - r)/r*100
if OS < 0:
    OS = 0
print("The percent overshoot is {0:.1f}%".format(OS))

print ("The steady state offset at 30 seconds is {0:.3f} meters".format(abs(soln[-1,0]-r)))

##################################################################################
# Your goal is to follow the comments and complete the the tasks asked of you.
#
# Good luck designing your proportional integral controller!
#
##################################################################################


class PI_Controller:
    def __init__(self, kp = 0.0, ki = 0.0, start_time = 0):
        
        # The PI controller can be initalized with a specific kp value
        # and ki value
        self.kp_ = float(kp)
        self.ki_ = float(ki)

        # Define error_sum_ and set to 0.0
        ########################################

        ########################################

        # Store relevant data
        self.last_timestamp_ = 0.0
        self.set_point_ = 0.0
        self.start_time_ = start_time

        # Control effort history
        self.u_p = [0]
        self.u_i = [0]

    def setTarget(self, target):
        self.set_point_ = float(target)

    def setKP(self, kp):
        self.kp_ = float(kp)
        
    def setKI(self, ki):
        # Set the internal ki_ value with the provided variable
        ########################################

        ########################################

    def update(self, measured_value, timestamp):
        delta_time = timestamp - self.last_timestamp_
        if delta_time == 0:
            # Delta time is zero
            return 0
        
        # Calculate the error 
        error = self.set_point_ - measured_value
        
        # Set the last_timestamp_ 
        self.last_timestamp_ = timestamp

        # Calculate the error_sum_
        ########################################

        ########################################
        
        # Proportional error
        p = self.kp_ * error
       
        # Calculate the integral error here. Be sure to access the 
        # the internal Ki class variable
        ########################################
        i = None
        ########################################
        
        # Set the control effort
        # u is the sum of all your errors. In this case it is just 
        # the proportional and integral error.
        ########################################
        u = None
        ########################################
        
        # Here we are storing the control effort history for post control
        # observations. 
        self.u_p.append(p)
        self.u_i.append(i)

        return u

import numpy as np
import matplotlib.pyplot as plt
from pi_controller import PI_Controller

##################################################################################
## DO NOT MODIFY ANY PORTION OF THIS FILE
##################################################################################

def ydot(y, t, pi):
    ''' Returns the state vector at the next time-step

    Parameters:
    ----------
    y(k) = state vector, a length 2 list
      = [altitude, speed]
    t = time, (sec)
    pid = instance of the PIDController class

    Returns
    -------
    y(k+1) = [y[0], y[1]] = y(k) + ydot*dt
    '''

    # Model state
    y0 = y[0] # altitude, (m)
    y1 = y[1] # speed, (m/s)


    # Model parameters
    g = -9.81 # gravity, m/s/s
    m =  1.54 # quadrotor mass, kg
    c =  10.0 # electro-mechanical transmission constant

    # time step, (sec)
    dt = t - pi.last_timestamp_
    # Control effort
    u = pi.update(y0,t)

    ### State derivatives
    # if altitude = 0
    if (y0 <= 0.):
        # if control input, u <= gravity, vehicle stays at rest on the ground
        # this prevents quadrotor from "falling" through the ground when thrust is
        # too small.
        if u <= np.absolute(g*m/c):
            y0dot = 0.
            y1dot = 0.
        else:  # else if u > gravity and quadrotor accelerates upwards
            y0dot = y1
            y1dot = g + c/m*u - 0.75*y1
    else: # otherwise quadrotor is already in the air
        y0dot = y1
        y1dot = g + c/m*u - 0.75*y1

    y0 += y0dot*dt
    y1 += y1dot*dt
    return [y0, y1]

##################################################################################
# Your goal is to follow the comments and complete the the tasks asked of you.
#
# Good luck designing your proportional integral controller!
#
##################################################################################

class PI_Controller:
    def __init__(self, kp = 0.0, ki = 0.0, start_time = 0):
        
        # The PI controller can be initalized with a specific kp value
        # and ki value
        self.kp_ = float(kp)
        self.ki_ = float(ki)

        # Define error_sum_ and set to 0.0
        ########################################
        self.error_sum_ = 0.0
        ########################################

        # Store relevant data
        self.last_timestamp_ = 0.0
        self.set_point_ = 0.0
        self.start_time_ = start_time

        # Control effort history
        self.u_p = [0]
        self.u_i = [0]

    def setTarget(self, target):
        self.set_point_ = float(target)

    def setKP(self, kp):
        self.kp_ = float(kp)
        
    def setKI(self, ki):
        # Set the internal ki_ value with the provided variable
        ########################################
        self.ki_ = float(ki)
        ########################################

    def update(self, measured_value, timestamp):
        delta_time = timestamp - self.last_timestamp_
        if delta_time == 0:
            # Delta time is zero
            return 0
        
        # Calculate the error 
        error = self.set_point_ - measured_value
        
        # Set the last_timestamp_ 
        self.last_timestamp_ = timestamp

        # Calculate the error_sum_
        ########################################
        self.error_sum_ += error * delta_time
        ########################################
        
        # Proportional error
        p = self.kp_ * error
       
        # Calculate the integral error here. Be sure to access the 
        # the internal Ki class variable
        ########################################
        i = self.ki_ * self.error_sum_
        ########################################
        
        # Set the control effort
        # u is the sum of all your errors. In this case it is just 
        # the proportional and integral error.
        ########################################
        u = p + i
        ########################################
        
        # Here we are storing the control effort history for post control
        # observations. 
        self.u_p.append(p)
        self.u_i.append(i)

        return u

Reflect

QUESTION:

Take some time after you have played with the code above to reflect on these questions:

What happens when Ki is large?
What happens when Ki is small?
Do we reach our desired goal?
How does control effort vary with different Ki values?
How does the steady state offset and overshoot vary with different Ki values?

ANSWER:

There is no desired answer to this question but hopefully taking time to reflect on these questions will give you a deeper understanding of the integral "knob"!

Check your understanding!

QUIZ QUESTION::

Can you match up the expected result with an increase of the integral constant?

ANSWER CHOICES:

Objective	Answer
Decrease
Increase
Increase
Decrease
Degrade

SOLUTION:

Objective	Answer
Decrease
Decrease
Increase
Increase
Increase
Increase
Decrease
Decrease
Degrade